Unit 1 rigid transformations and congruence – Unit 1: Rigid Transformations and Congruence explores the fundamental concepts of geometry, laying a solid foundation for understanding the properties and relationships of shapes. Through a comprehensive examination of rigid transformations and congruence, this unit equips learners with the tools to analyze, manipulate, and prove geometric relationships.
This unit delves into the different types of rigid transformations, including translation, rotation, and reflection, and their impact on geometric figures. The concept of congruence is thoroughly examined, establishing the criteria for determining whether two figures are congruent and the properties that define congruent figures.
Rigid Transformations and Congruence: Unit 1 Rigid Transformations And Congruence

In geometry, rigid transformations are transformations that preserve the distance and orientation of figures. They are used to describe the movement of figures without changing their shape or size. Congruence is a relationship between two figures that have the same shape and size.
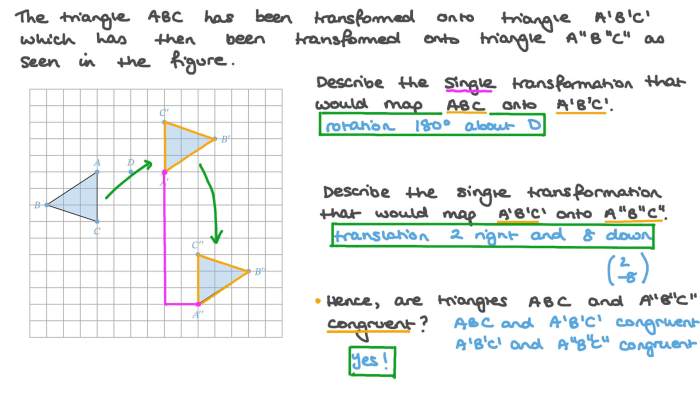
Rigid transformations can be used to prove that two figures are congruent.
Rigid Transformations
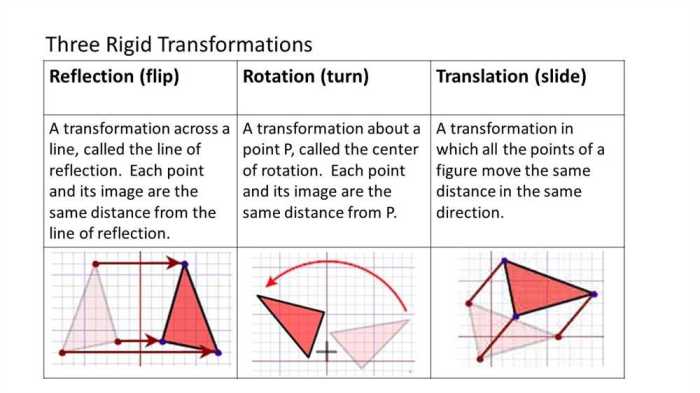
Rigid transformations are transformations that preserve the distance and orientation of figures. The three types of rigid transformations are translation, rotation, and reflection.
- Translationis a transformation that moves a figure from one point to another without changing its orientation.
- Rotationis a transformation that turns a figure around a fixed point.
- Reflectionis a transformation that flips a figure over a line.
Congruence
Congruence is a relationship between two figures that have the same shape and size. Two figures are congruent if they can be superimposed on each other so that every point of one figure coincides with a point of the other figure.
The conditions for congruence are:
- The corresponding sides of the figures are equal in length.
- The corresponding angles of the figures are equal in measure.
Properties of Rigid Transformations and Congruence, Unit 1 rigid transformations and congruence
Rigid transformations have the following properties:
- They preserve distance.
- They preserve orientation.
Rigid transformations can be used to prove that two figures are congruent. If two figures can be obtained from each other by a sequence of rigid transformations, then they are congruent.
Applications of Rigid Transformations and Congruence
Rigid transformations and congruence have many applications in real-world scenarios, such as:
- Architecture: Architects use rigid transformations to design buildings and other structures.
- Engineering: Engineers use rigid transformations to design machines and other objects.
- Geometry: Congruence is a fundamental concept in geometry. It is used to prove theorems and solve problems.
General Inquiries
What are rigid transformations?
Rigid transformations are transformations that preserve the distance and orientation of a figure. They include translation, rotation, and reflection.
What is congruence?
Congruence is a relationship between two figures that have the same size and shape. Congruent figures can be superimposed on each other exactly.
How can rigid transformations be used to prove congruence?
Rigid transformations can be used to prove congruence by showing that two figures can be transformed into each other through a series of rigid transformations.